10 Paradoxes qui embrouilleront ton esprit pendant un moment

La logique et le bon sens sont généralement nos meilleurs outils lorsqu’il s’agit de résoudre des situations théoriques. Ils nous aident à trouver la solution la plus adaptée au problème en question. Cependant, les paradoxes mettent notre esprit à l’épreuve, car leur résolution ressemble davantage à un labyrinthe sans issue. Ces dilemmes semblent ne pas avoir de solution et c’est aussi pour cela qu’ils sont fascinants.

Sympa a compilé pour toi une liste des paradoxes les plus célèbres afin de faire un peu fumer ton cerveau.

1. Le paradoxe des corbeaux

Également connue sous le nom de “paradoxe de Hempel”, cette théorie a été proposée par le philosophe Carl Hempel. Son objectif était de prouver que lorsque des événements coïncident avec les limites d’une théorie, notre confiance en cette théorie augmente considérablement. Pour illustrer son argumentation, il a donné comme exemple la théorie selon laquelle “tous les corbeaux sont noirs”.

Si nous regardons des millions de corbeaux et que nous constatons que chacun d’entre eux est noir, nous croirons un peu plus à cette affirmation à chaque nouvelle observation de corbeau noir. Et si on va plus loin dans cette observation, on peut alors affirmer que tout ce qui n’est pas noir n’est pas un corbeau. Donc si on regarde une pomme de couleur rouge, et qu’on se dit que n’étant pas noire, elle ne peut pas être un corbeau, la conviction que tous les corbeaux sont noirs est alors d’autant plus grande.

2. Le paradoxe d’Épiménide

À l’époque de la Grèce Antique, un homme nommé Épiménide affirmait que tous les Crétois étaient des menteurs. Cela pourrait passer pour une simple accusation, mais étant lui-même Crétois, s’il disait la vérité, ça voulait dire qu’au moins un Crétois n’était pas un menteur, donc son affirmation était alors fausse.

Et s’il mentait, affirmer que tous les Crétois étais des menteurs était également faux, donc dans tous les cas, sa déclaration est fausse, ce qui est en fait la solution du paradoxe (tu suis?).

3. Le paradoxe d’Abilene

Ce paradoxe social a été proposé par le sociologue Jerry Harvey, dans son livre The Abilene Paradox and Other Meditations on Management.

Dans cet exemple, une famille composée de deux couples, les mariés et leurs beaux-parents, jouent paisiblement aux dominos sous le porche par une chaude journée d’été.
Le beau-père propose de se rendre à Abilene, une ville située à 80 km de l’endroit où ils se trouvent, pour dîner. La jeune femme répond que c’est une bonne idée, bien que secrètement, elle n’en est pas convaincue, car il fait très chaud. Mais elle croit être la seule à penser ça. Son mari est également d’accord, à condition que sa belle-mère ait envie d’y aller. Cette dernière acquiesce, et ils se mettent en route. Comme l’avait prédit la femme, le voyage est long, chaud et fatiguant.

Arrivés à Abilene, la nourriture du restaurant s’avère aussi mauvaise que le voyage, et toute la famille décide de rentrer chez elle après quelques heures. Sur le chemin du retour, la femme mentionne sur un ton sarcastique que ce voyage n’était pas une très bonne idée. Son mari lui répond qu’il a accepté uniquement pour faire plaisir à sa belle-mère, qui répond qu’elle n’avait pas vraiment d’opinion à ce sujet, et le beau-père dit qu’il a suggéré ce voyage parce que tout le monde avait l’air de s’ennuyer.

Toute la famille a donc pris ensemble une décision qui ne plaisait à personne. Jerry Harvey essaie de nous expliquer par cet exemple comment certaines situations nous poussent à faire des choses qui ne découlent pas forcément de notre volonté.

4. Le chat de Schrödinger

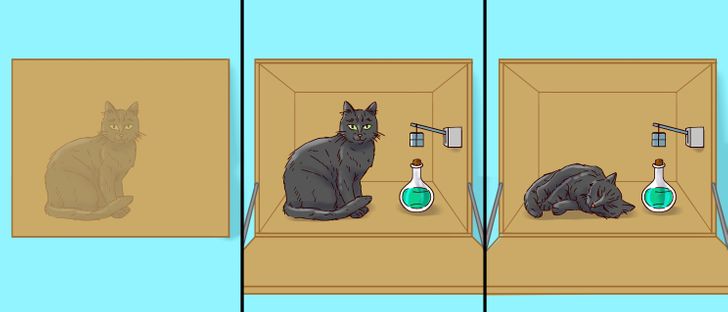
Le physicien autrichien Erwin Schrödinger a créé un système composé d’une boîte opaque contenant un chat, un flacon de poison, et un dispositif doté d’une seule particule radioactive qui avait seulement une chance sur deux d’exploser. Le chat avait donc 50% de chances de survivre en étant enfermé dans cette boîte.

Tout comme les électrons ont la capacité de se trouver à deux endroits en même temps, Schrödinger voulait démontrer ici que les éléments indiquant si le chat est vivant ou mort pouvaient présenter les deux résultats en même temps. En effet, ce n’est qu’en ouvrant la boîte que l’on peut savoir si le chat est vivant ou mort. Mais tant que la boîte reste fermée, les deux affirmations sont tout aussi correctes l’une que l’autre. Le chat est à la fois vivant et mort, ce qui donne lieu à un paradoxe.

5. Le paradoxe du grand-père

Ce dilemme est également connu sous le nom de “paradoxe du voyage dans le temps”, et il a été exposé en 1943 par l’auteur de science-fiction René Barjavel, dans le cadre de son roman Le voyageur imprudent. Dans ce livre, il parle d’un homme qui voyage dans le passé et tue son grand-père, le père de son père biologique.

Si son grand-père était mort dans le passé, l’assassin n’aurait jamais été conçu, et dans ce cas, il est donc impossible qu’il ait tué son grand-père. Ou bien peut-être que le grand-père a survécu, permettant ainsi au voyageur d’être conçu, etc....

6. Le paradoxe du barbier

Ce dilemme, également nommé “paradoxe de Russell”, démontre la théorie des ensembles, et est justement attribué à Bertrand Russell, philosophe, mathématicien et écrivain. Ce dilemme raconte l’histoire d’As-Samet, le barbier d’un ancien émirat, qui était très doué dans son travail. Un jour, l’émir ordonna qu’en raison du manque de barbiers, les barbiers existants ne pouvaient raser que les hommes incapables de se raser eux-mêmes.

Pendant qu’As-Samet rasait l’émir, il lui confia que, dans son empressement à se conformer à la loi, il se trouvait face à un grand dilemme. Il était le seul barbier de son village, et ne pouvait pas se raser, car selon la loi, il n’en avait pas le droit. Pour l’émir, cette pensée semblait si profonde qu’il donna à As-Samet la main d’une de ses filles.

7. Le paradoxe des jumeaux

Ce dilemme a été exposé par Albert Einstein pour expliquer la théorie de la relativité, en établissant que la mesure du temps n’est pas absolue, puisqu’elle dépend du mouvement et de la perspective du spectateur. Ce paradoxe est basé sur l’histoire de deux frères jumeaux, dont l’un effectuerait un long voyage interstellaire à grande vitesse, pendant que l’autre resterait sur Terre pendant environ 20 ans.

Cette théorie indique que le jumeau qui serait resté sur Terre vieillirait plus vite à cause de la dilatation du temps, c’est-à-dire qu’il verrait le temps passer plus lentement. De son côté, le jumeau qui serait parti dans l’espace reviendrait plus jeune, car ayant voyagé à très grande vitesse, le temps semblerait s’être écoulé plus vite pour lui. Tout ceci est possible parce que le temps est relatif.

8. L’hôtel infini de Hilbert

Pour expliquer les faits paradoxaux et le concept d’infini en mathématiques, David Hilbert a pris comme exemple l’histoire de deux grands hôteliers qui avaient l’ambition de construire le plus grand hôtel du monde. En se demandant combien de chambres ils devaient prévoir, ils ont rapidement conclu que si quelqu’un d’autre construisait un jour un hôtel avec plus de chambres, ils n’auraient plus le plus grand hôtel du monde. Ils ont donc décidé de construire un hôtel avec un nombre de chambres infini.

Quand ils ont ouvert les portes de l’Hôtel Infini, ce dernier devint vite très populaire, de sorte que son infinité de chambres s’est vite retrouvée occupée par une infinité de clients. Mais cela voulait aussi dire qu’il n’y avait plus de place pour accueillir un client de plus. Pour résoudre ce problème et faire en sorte qu’aucun client ne se retrouve sans chambre, ils demandèrent à chaque client d’ajouter 1 à son numéro de chambre, et d’y emménager. Ainsi, la personne de la chambre 1 passait à la chambre 2, la personne de la chambre 2 passait à la chambre 3, et ainsi de suite, de sorte que la chambre nº1 restait toujours disponible.

Quelque temps plus tard, un nouveau nombre infini de clients arrivèrent, et une fois de plus, les hôteliers ont trouvé la solution pour tous les accueillir. Ils ont alors demandé à tous les clients présents de multiplier par deux le numéro de leurs chambres, de telle sorte que chacun occupe désormais une chambre de numéro pair. Le client de la chambre 1 passa ainsi à la 2, celui de la 2 passa à la 4, celui de la 3 passa à la 6, etc... Ainsi, une infinité de chambres de nombres impairs devenaient disponibles, et cette nouvelle infinité de clients pouvait alors les occuper.

9. Le paradoxe du crocodile

Ce paradoxe a été utilisé pour démontrer les problèmes de logique de raisonnement pour deviner ce qui pourrait arriver, sachant ce que nous savons déjà. Ce dilemme est illustré par l’histoire d’un crocodile qui enlève un enfant dans les bras de sa mère. Le crocodile promet à la femme qu’il lui rendra son enfant si elle arrive à deviner ce qu’il va faire de lui.

La mère lui répond alors qu’il va le manger, ce qui crée un dilemme pour le reptile. Si le crocodile dévore l’enfant, la mère aura deviné juste et le crocodile devra rendre l’enfant. Si le crocodile rend l’enfant, la mère se sera trompée et le crocodile devra le dévorer. Et si le crocodile décide de laisser partir l’enfant, c’est la mère qui aura tort, mais elle récupérera quand même son enfant.

10. Le bateau de Thésée

Selon la légende grecque, après que Thésée et son équipage sont revenus de Crète, les Athéniens conservèrent son immense navire en remplaçant progressivement chaque pièce usée par une nouvelle, de telle sorte que plusieurs générations après, ce bateau était toujours aussi resplendissant.

Ceci a fini par diviser les philosophes, qui se demandaient si on pouvait toujours considérer que ce bateau était celui de Thésée, ou si une fois toutes les pièces changées, on devait plutôt considérer que ce navire était tout simplement un autre. Mais dans ce cas, alors, où était passé le bateau de Thésée ? Et à quel moment avait-il cessé de l’être ?

Penses-tu avoir la solution à l’un de ces dilemmes ? Connais-tu d’autres paradoxes qui t’ont torturé l’esprit pendant des heures ? Fais-nous part de tes pensées dans les commentaires, et n’hésite pas à partager cet article avec les personnes de ton entourage !